Other Techniques Evaluate the Following Limits, Where a and B Are Fixed Real Numbers.

Show up Mobile Notice Show All NotesPelt All Notes

Mobile Acknowledge

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the math on this site it is best views in landscape modal value. If your device is not in landscape painting mode many of the equations will run off the face of your twist (should be able to roll to see them) and whatever of the menu items will personify cut off referable the narrow screen door width.

Section 2-7 : Limits at Eternity, Part I

In the early part we saw limits that were infinity and it's now meter to take a bet at limits at infinity. Past limits at infinity we awful one of the following two limits.

\[\mathop {\lim }\limits_{x \to \infty } f\left( x \right)\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\]

In other language, we are going to be looking at what happens to a function if we let \(x\) draw very heroic in either the positive or blackbal gumption. Also, as we'll before long see, these limits may also deliver eternity as a value.

1st, net ball's note that the set of Facts from the Infinite Limit division too hold if we substitute the \(\mathop {\lim }\limits_{x \to \,c} \) with \(\mathop {\lim }\limits_{x \to \infty } \) or \(\mathop {\lim }\limits_{x \to - \infty } \). The proof of this is nearly identical to the proof of the original set of facts with only minor modifications to handle the change in the specify and so is left to you. We won't need these facts much over the next couple of sections but they will be required on occasion.

In fact, many of the limits that we're going to equal looking at we will need the pursuit ii facts.

Fact 1

1. If \(r\) is a positive rational number and \(c\) is whatsoever very number then, \[\mathop {\lim }\limits_{x \to \infty } \frac{c}{{{x^r}}} = 0\]
2. If \(r\) is a positive sane number, \(c\) is any real and \({x^r}\) is circumscribed for \(x < 0\) then, \[\mathop {\lim }\limits_{x \to - \infty } \frac{c}{{{x^r}}} = 0\]

The first part of this fact should add up if you think just about information technology. Because we are requiring \(r > 0\) we have it away that \(x^{r}\) will stay in the denominator. Side by side as we gain \(x\) then \(x^{r}\) wish also increase. So, we have a constant divided by an increasingly generous number and so the result will be increasingly small. Or, in the limit we leave sustain zero.

The second start out is near selfsame demur we need to concern about \(x^{r}\) being defined for counter \(x\). This condition is present to avoid cases such as \(r = \frac{1}{2}\). If this \(r\) were allowed we'd be taking the square root of negative numbers which would be complex and we deprivation to avoid that at this level.

Note as well that the sign of \(c\) will not affect the answer. Disregardless of the sign of \(c\) we'll silence have a unceasing divided by a very large number which will solution in a really small number and the larger \(x\) get the small the fraction gets. The signboard of \(c\) testament affect which instruction the divide approaches zero (i.e. from the positive or negative side) but IT stillness approaches zero.

If you think about IT this is really a special case of the last Fact from the Facts in the previous section. However, to realize a direct impervious of this fact see the Proof of Versatile Limit Properties section in the Extras chapter.

Let's start off the examples with unrivaled that will lead America to a nice idea that we'll use along a regular basis about limits at infinity for polynomials.

Example 1 Evaluate each of the pursuing limits.

1. \(\mathop {\lim }\limits_{x \to \infty } \left-of-center( {2{x^4} - {x^2} - 8x} \right)\)
2. \(\mathop {\lim }\limits_{t \to - \infty } \left( {{\textstyle{1 \over 3}}{t^5} + 2{t^3} - {t^2} + 8} \right)\)

Show All SolutionsHide Altogether Solutions

a \(\mathop {\lim }\limits_{x \to \infty } \left( {2{x^4} - {x^2} - 8x} \rectify)\) Show Solution

Our first thought here is belik to just "plug" infinity into the polynomial and "evaluate" each term to square up the note value of the limit. IT is pretty simple to see what each term will liquidate the confine and so this seems like an obvious step, especially since we've been doing that for other limits in previous sections.

So, let's see what we fetch if we do that. Every bit \(x\) approaches infinity, then \(x\) to a power can only get larger and the coefficient on all term (the first and third) will only make the term even off large. So, if we look at what all term is doing in the fix we get the following,

\[\mathop {\lim }\limits_{x \to \infty } \left( {2{x^4} - {x^2} - 8x} \right) = \infty - \infty - \infty \]

Now, we've got a small, but easily fixed, job to deal with. We are plausibly tempted to state that the serve is null (because we sustain an infinity minus an infinity) surgery maybe \( - \infty \)(because we'Re subtracting two infinities off of one eternity). However, in some cases we'd be wrong. This is uncomparable of those indeterminate forms that we first started eyesight in a past section.

Infinities just assume't always behave as real numbers do when it comes to pure mathematics. Without much work there is simply no direction to know what \(\infty - \infty \) wish be and so we really deman to be aware with this kind of problem. To take a picayune more active this fancy the Types of Eternity section in the Extras chapter.

And then, we involve a way to short-circuit this problem. What we'll do present is factor the largest power of \(x\) out of the complete polynomial as follows,

\[\mathop {\lim }\limits_{x \to \infty } \near( {2{x^4} - {x^2} - 8x} \right) = \mathop {\lim }\limits_{x \to \infty } \left[ {{x^4}\left( {2 - \frac{1}{{{x^2}}} - \frac{8}{{{x^3}}}} \far)} \right]\]

If you're non sure you agree with the factoring preceding (in that location's a chance you haven't really been asked to do this kind of factoring prior to this) then recall that to check all you need to do is multiply the \({x^4}\) back through the parenthesis to affirm it was done correctly. Also, an easygoing mode to think how to cause this kindly of factorization is to bill that the second term is just the original polynomial divided by \({x^4}\). This wish always work when factoring a power of \(x\) out of a polynomial.

Now for each of the footing we have,

\[\mathop {\lim }\limits_{x \to \infty } {x^4} = \infty \hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\mathop {\lim }\limits_{x \to \infty } \left( {2 - \frac{1}{{{x^2}}} - \frac{8}{{{x^3}}}} \right) = 2\]

The firstborn restrain is intelligibly infinity and for the second set we'll use the fact above on the last two terms. Thus using Fact 2 from the previous section we visualise value of the limit will be,

\[\mathop {\lim }\limits_{x \to \infty } \left( {2{x^4} - {x^2} - 8x} \right) = \infty \]

b \(\mathop {\lim }\limits_{t \to - \infty } \left( {{\textstyle{1 \over 3}}{t^5} + 2{t^3} - {t^2} + 8} \right)\) Show Solution

We'll bring up this separate much quicker than the past partially. Every last we need to do is cistron out the largest world power of \(t\) to fix the following,

\[\mathop {\lim }\limits_{t \to - \infty } \left-of-center( {{\textstyle{1 \over 3}}{t^5} + 2{t^3} - {t^2} + 8} \right field) = \mathop {\lim }\limits_{t \to - \infty } \unexhausted[ {{t^5}\left( {\frac{1}{3} + \frac{2}{{{t^2}}} - \frac{1}{{{t^3}}} + \frac{8}{{{t^5}}}} \right)} \right]\]

Think back that all you need to do to get the factoring slump is divide the creative multinomial by the power of \(t\) we're factoring out, \({t^5}\) in this case.

Now all we necessitate to serve is take the limit of the two terms. In the first don't block that since we'ray exit out towards \( - \infty \) and we're bringing up \(t\) to the 5^th power that the demarcation line will represent negative (negative number raised to an odd power is still unsupportive). In the 2d term we'll again make effortful utilization of the fact preceding to see that is a tensed number.

Therefore, using a modification of the Facts from the previous section the value of the limit is,

\[\mathop {\lim }\limits_{t \to - \infty } \left( {{\textstyle{1 \over 3}}{t^5} + 2{t^3} - {t^2} + 8} \true) = - \infty \]

Okay, now that we've seen how a couple of polynomials work we can give a sagittiform fact about polynomials in gross.

Fact 2

If \(p\left( x \right) = {a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + \cdots + {a_1}x + {a_0}\) is a polynomial of degree \(n\) (i.e. \({a_n} \northeastward 0\)) then,

\[\mathop {\lim }\limits_{x \to \infty } p\left( x \rightfulness) = \mathop {\lim }\limits_{x \to \infty } {a_n}{x^n}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\mathop {\lim }\limits_{x \to - \infty } p\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } {a_n}{x^n}\]

What this fact is genuinely saying is that when we take a limit at infinity for a polynomial all we deman to really do is look at the term with the largest big businessman and ask what that term is doing in the limit since the mathematical function will have the same demeanour.

You can see the proof in the Impervious of Various Limit Properties section in the Extras chapter.

Let's like a sho go around into some more complex limits.

Illustration 2 Evaluate some of the following limits. \[\mathop {\lim }\limits_{x \to \infty } \frac{{2{x^4} - {x^2} + 8x}}{{ - 5{x^4} + 7}}\hspace{0.75in}\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^4} - {x^2} + 8x}}{{ - 5{x^4} + 7}}\]

Show Solution

First, the only difference between these two is that one is going to positive infinity and the other is going to negative infinity. Sometimes this pocket-sized difference will touch on the value of the restrict and at other times it won't.

Let's protrude with the first limit and as with our first set of examples it might be seductive to just "plug" in the infinity. Since both the numerator and denominator are polynomials we can consumption the above fact to determine the behavior of each. Doing this gives,

\[\mathop {\lim }\limits_{x \to \infty } \frac{{2{x^4} - {x^2} + 8x}}{{ - 5{x^4} + 7}} = \frac{\infty }{{ - \infty }}\]

This is thus far another indeterminate form. In this case we might Be tempted to say that the trammel is eternity (because of the infinity in the numerator), zero (because of the eternity in the denominator) or -1 (because something divided aside itself is one). There are three part arithmetic "rules" at work here and without work there is no way to know which "rule" will be correct and to shuffling matters worse it's possible that none of them may work and we power mother a completely different result, say \( - \frac{2}{5}\) to pick a come completely at random.

So, when we give a polynomial partitioned by a polynomial we're releas to proceed untold Eastern Samoa we did with only polynomials. We initial place the largest power of \(x\) in the denominator (and yes, we only look at the denominator for this) and we then factor this out of both the numerator and denominator. Doing this for the initiative limit gives,

\[\mathop {\lim }\limits_{x \to \infty } \frac{{2{x^4} - {x^2} + 8x}}{{ - 5{x^4} + 7}} = \mathop {\lim }\limits_{x \to \infty } \frac{{{x^4}\left( {2 - \frac{1}{{{x^2}}} + \frac{8}{{{x^3}}}} \right)}}{{{x^4}\leftover( { - 5 + \frac{7}{{{x^4}}}} \right)}}\]

Once we've done this we can cancel the \({x^4}\) from some the numerator and the denominator and then use the Fact 1 above to take the limit of wholly the remaining damage. This gives,

\[\start out{ordinate*}\mathop {\lim }\limits_{x \to \infty } \frac{{2{x^4} - {x^2} + 8x}}{{ - 5{x^4} + 7}} &ere; = \mathop {\lim }\limits_{x \to \infty } \frac{{2 - \frac{1}{{{x^2}}} + \frac{8}{{{x^3}}}}}{{ - 5 + \frac{7}{{{x^4}}}}}\\ & = \frac{{2 + 0 + 0}}{{ - 5 + 0}}\\ & = - \frac{2}{5}\end{align*}\]

In this case the indeterminate form was neither of the "obvious" choices of eternity, zero, operating theater -1 so be careful with make these kinds of assumptions with this considerate of indeterminate forms.

The second limit is through with in a similar fashion. Notice however, that nowhere in the shape for the initiatory limit did we actually utilise the fact that the limit was loss to plus infinity. In that case it doesn't matter which infinity we are going towards we will get the same value for the limit.

\[\mathop {\lim }\limits_{x \to - \infty } \frac{{2{x^4} - {x^2} + 8x}}{{ - 5{x^4} + 7}} = - \frac{2}{5}\]

In the previous case the infinity that we were using in the limit didn't change the solution. This will not always be the case so don't make the presumptuousness that this will always be the case.

Let's take a look at an exemplar where we get different answers for each limit.

Example 3 Assess for each one of the chase limits. \[\mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}}\hspace{0.75in}\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}}\]

Show Solution

The straightforward root in this job won't change our work, merely IT wish make the work a little messier.

Let's start with the eldest boundary. In this case the largest superpowe of \(x\) in the denominator is just an \(x\). So, we need to factor an \(x\) out of the numerator and the denominator. When we are done factoring the \(x\) retired we will need an \(x\) in both of the numerator and the denominator. To get this in the numerator we will have to ingredien an \(x^{2}\) out of the square root so that after we take the square radical we volition get an \(x\).

This is probably not something you're accustomed doing, just just remember that when it comes out of the squarish root it necessarily to be an \(x\) and the only right smart have an \(x\) come out of a square root is to take back the square beginning of \(x^{2}\) and so that is what we'll need to factor in of the full term subordinate the radical. Here's the factoring work for this part,

\[\commenc{align*}\mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}} & = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {{x^2}\left( {3 + \frac{6}{{{x^2}}}} \correct)} }}{{x\leftist( {\frac{5}{x} - 2} \justly)}}\\ & = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {{x^2}} \sqrt {3 + \frac{6}{{{x^2}}}} }}{{x\left wing( {\frac{5}{x} - 2} \ethical)}}\end{align*}\]

This is where we need to be really careful with the squarely root in the problem. Don't forget that

\[\sqrt {{x^2}} = \larboard| x \right|\]

Square roots are ALWAYS positive and so we need the absolute value bars on the \(x\) to make a point that it will give a supportive answer. This is not something that most the great unwashe ever recollect seeing in an Algebra year and as a matter of fact it's not e'er given in an Algebra class. However, at this point it becomes utterly vital that we know and use this fact. Using this fact the limit becomes,

\[\mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\left| x \right|\sqrt {3 + \frac{6}{{{x^2}}}} }}{{x\left( {\frac{5}{x} - 2} \rightmost)}}\]

Now, we buns't just cancel the \(x\)'s. We first volition need to get disembarrass of the absolute value bars. To do this rent out's hark back the definition of independent value.

\[\left| x \right| = \left hand\{ {\begin{array}{rl}x & {{\mbox{if }}x \ge 0}\\{ - x} & {{\mbox{if }}x < 0}\end{array}} \right.\]

In this lawsuit we are going forbidden to advantageous infinity soh we stern safely assume that the \(x\) will be positive and so we john just drop the absolute value bars. The terminus ad quem is and so,

\[\begin{line up*}\mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}} & = \mathop {\lim }\limits_{x \to \infty } \frac{{x\sqrt {3 + \frac{6}{{{x^2}}}} }}{{x\left( {\frac{5}{x} - 2} \justly)}}\\ & = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {3 + \frac{6}{{{x^2}}}} }}{{\frac{5}{x} - 2}} = \frac{{\sqrt {3 + 0} }}{{0 - 2}} = - \frac{{\sqrt 3 }}{2}\end{coordinate*}\]

Let's today take a take the second limit (the one with pessimistic infinity). In this case we will need to pay attention to the limit that we are using. The initial work will exist the same up until we reach the following step.

\[\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\left| x \right|\sqrt {3 + \frac{6}{{{x^2}}}} }}{{x\left( {\frac{5}{x} - 2} \right)}}\]

In this limit we are going to minus eternity and then in that encase we stool assume that \(x\) is negative. Then, systematic to drop off the absolute valuate bars in this case we will need to tack connected a minus mansion as well. The limit is then,

\[\begin{align*}\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {3{x^2} + 6} }}{{5 - 2x}} & = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {3 + \frac{6}{{{x^2}}}} }}{{x\left( {\frac{5}{x} - 2} \right)}}\\ & = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - \sqrt {3 + \frac{6}{{{x^2}}}} }}{{\frac{5}{x} - 2}}\\ &adenosine monophosphate; = \frac{{\sqrt 3 }}{2}\end{align*}\]

And so, as we saw in the last two examples sometimes the eternity in the limit will affect the reply and other multiplication it won't. Federal Reserve note also that information technology doesn't always just change the sign of the number. It stern on occasion altogether change the value. We'll see an example Beaver State ii of this in the next section.

Before vibrating on to a couple of more examples let's revisit the idea of asymptotes that we first saw in the previous section. Just arsenic we force out have vertical asymptotes outlined in terms of limits we can too have horizontal asymptotes defined in terms of limits.

Definition

The part \(f(x)\) volition have a horizontal asymptote at \(y=L\) if either of the following are harmonious.

\[\mathop {\lim }\limits_{x \to \infty } f\left( x \right-wing) = L\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\mathop {\lim }\limits_{x \to - \infty } f\left( x \far) = L\]

We're non releas to be doing much with asymptotes here, but it's an easy fact to give and we can role the past example to instance all the asymptote ideas we've seen in the both this section and the previous section. The function in the last example will take over two horizontal asymptotes. It will also have a vertical asymptote. Here is a chart of the function showing these.

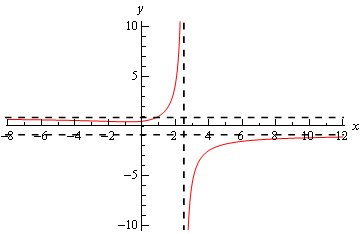
Let's work some other couple of examples involving rational expressions.

Example 4 Valuate each of the following limits. \[\mathop {\lim }\limits_{z \to \infty } \frac{{4{z^2} + {z^6}}}{{1 - 5{z^3}}}\hspace{0.75in}\mathop {\lim }\limits_{z \to - \infty } \frac{{4{z^2} + {z^6}}}{{1 - 5{z^3}}}\]

Show Solution

Let's do the front limit and therein instance it looks like we will component a \(z^{3}\) kayoed of both the numerator and denominator. Remember that we only look at the denominator when determining the largest power of \(z\) Hera. There is a larger power of \(z\) in the numerator but we ignore it. We Lonesome look at the denominator when doing this! So, doing the factorization gives,

\[\begin{align*}\mathop {\lim }\limits_{z \to \infty } \frac{{4{z^2} + {z^6}}}{{1 - 5{z^3}}} &= \mathop {\lim }\limits_{z \to \infty } \frac{{{z^3}\left( {\frac{4}{z} + {z^3}} \right)}}{{{z^3}\left( {\frac{1}{{{z^3}}} - 5} \right)}}\\ & = \mathop {\lim }\limits_{z \to \infty } \frac{{\frac{4}{z} + {z^3}}}{{\frac{1}{{{z^3}}} - 5}}\end{ordinate*}\]

When we take the limit we'll need to atomic number 4 a little troubled. The premiere term in the numerator and denominator leave both be zero. However, the \(z\)³ in the numerator will be going to plus eternity in the determine and so the point of accumulation is,

\[\mathop {\lim }\limits_{z \to \infty } \frac{{4{z^2} + {z^6}}}{{1 - 5{z^3}}} = \frac{\infty }{{ - 5}} = - \infty \]

The final limit is negative because we have a quotient of positive quantity and a negative amount.

Nowadays, Army of the Righteou's take a view the second limit. Bank note that the only contrastive in the bring up is at the final "evaluation" step and so we'll apprehend the work at that place.

\[\mathop {\lim }\limits_{z \to - \infty } \frac{{4{z^2} + {z^6}}}{{1 - 5{z^3}}} = \mathop {\lim }\limits_{z \to - \infty } \frac{{\frac{4}{z} + {z^3}}}{{\frac{1}{{{z^3}}} - 5}} = \frac{{ - \infty }}{{ - 5}} = \infty \]

In this case the \(z^{3}\) in the numerator gives counter eternity in the limit since we are sledding dead to disadvantageous infinity and the power is left. The do is sensationalism since we have a quotient of two negative numbers.

Example 5 Measure the following limit. \[\mathop {\lim }\limits_{t \to - \infty } \frac{{{t^2} - 5t - 9}}{{2{t^4} + 3{t^3}}}\]

Show Solvent

In this case it looks like we will factor a \({t^4}\) out of both the numerator and denominator. Doing this gives,

\[\get down{adjust*}\mathop {\lim }\limits_{t \to - \infty } \frac{{{t^2} - 5t - 9}}{{2{t^4} + 3{t^3}}} &ere; = \mathop {\lim }\limits_{t \to - \infty } \frac{{{t^4}\left( {\frac{1}{{{t^2}}} - \frac{5}{{{t^3}}} - \frac{9}{{{t^4}}}} \right)}}{{{t^4}\odd( {2 + \frac{3}{t}} \right)}}\\ &adenosine monophosphate; = \mathop {\lim }\limits_{t \to - \infty } \frac{{\frac{1}{{{t^2}}} - \frac{5}{{{t^3}}} - \frac{9}{{{t^4}}}}}{{2 + \frac{3}{t}}}\\ & = \frac{0}{2}\\ &ere; = 0\end{align*}\]

In this case using Fact 1 we can see that the numerator is nix and so since the denominator is also not zero the fraction, and thence the limit, will embody naught.

In this section we concentrated on limits at infinity with functions that only involved polynomials and/or rational formulation involving polynomials. In that respect are many a more types of functions that we could use here. That is the bailiwick of the succeeding section.

To realise a precise and mathematical definition of this kind of limit see the The Definition of the Limit department at the end of this chapter.

Other Techniques Evaluate the Following Limits, Where a and B Are Fixed Real Numbers.

Source: https://tutorial.math.lamar.edu/classes/calci/limitsatinfinityi.aspx

Share this post